Anton wants to receive as a gift a rectangular table of size $n\times m$ filled with the numbers 0, 1, 2, 3, or 4.
Anton will be happy if there is no other "0" next to each "0", exactly one other "1" next to each "1", exactly two other "2"s next to each "2", exactly three other "3"s next to each "3", and exactly four other "4"s next to each "4" (i.e., all neighbors of "4" must also be "4").
One cell is considered to be next to another if they share a side.
You need to come up with a table that can be gifted to Anton so that he will be happy.
Below is an example of a table that will make Anton happy with $n=4, m=6$.
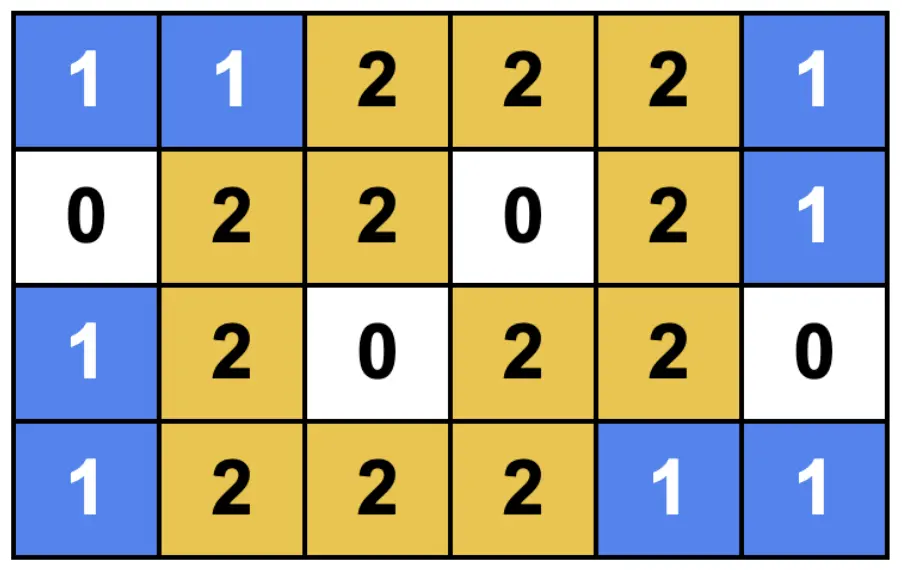
Input
A single line contains two numbers $n, m$ ($1 \leq n, m \leq 200$) --- the dimensions of the table.
It can be shown that a solution always exists.
Output
Output a table with $n$ rows and $m$ columns --- a gift for Anton.
Example
Input
4 6
Output
1 1 2 2 2 1 0 2 2 0 2 1 1 2 0 2 2 0 1 2 2 2 1 1
Scoring
- ($10$ points): $n = 1$;
- ($10$ points): $n = 2$;
- ($10$ points): $n = 3$;
- ($10$ points): $n = m = 4$;
- ($10$ points): $n = m = 30$;
- ($5$ points): $n = 30, m = 31$;
- ($5$ points): $n = 30, m = 32$;
- ($10$ points): $n = m = 31$;
- ($5$ points): $n = 31, m = 32$;
- ($10$ points): $n = m = 32$;
- ($15$ points): no additional restrictions.