Bajtłomieja czeka pierwsza w życiu podróż za ocean, do Stanów Zjednoczonych Bajtocji. Bardzo chce zobaczyć Bajhattan, dzielnicę jednego z tamtejszych ogromnych miast. Na Bajhattanie znajduje się mnóstwo wysokich wieżowców. Znana jest jego panorama, czyli widok na budynki z oddali.
Bajhattan składa się z $n \times m$ kwartałów. Każdy kwartał jest albo pusty, albo zajęty przez dokładnie jeden wieżowiec o pewnej wysokości. Dla uproszczenia, puste kwartały utożsamiamy z kwartałami zajętymi przez wieżowce o wysokości $0$. Pomijamy również ulice pomiędzy kwartałami. Przykładowo, dla $n = 3$, $m = 4$ oraz wysokości wieżowców jak w tabelce (widok z lotu ptaka, północ na górze tabelki)
| 1 | 2 | 0 | 3 |
| 1 | 0 | 1 | 2 |
| 2 | 1 | 0 | 1 |
Bajhattan wygląda jak na rysunku poniżej:
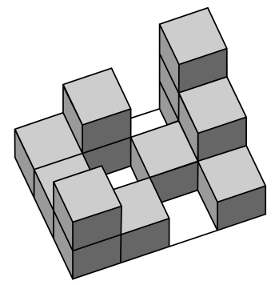
Bajtłomiej widział Bajhattan tylko na zdjęciach. Najbardziej znane są dwie panoramy, zachodnia oraz południowa. W przykładzie, w panoramie zachodniej wybijają się wieżowce o wysokościach 3, 2 oraz 2, a w panoramie południowej wieżowce o wysokościach 2, 2, 1 oraz 3. Zdjęcia były robione z dosyć daleka, więc widoczne są na nich jedynie zarysy budynków.
Dla układu wieżowców z przykładu, panorama zachodnia wygląda następująco:

A oto panorama południowa:

Bajtłomiej chciałby ustalić na podstawie zdjęć, jak duże są wieżowce na Bajhattanie. Chciałby oszacować ich objętość (kubaturę).
Pomóż mu i powiedz, jaka jest maksymalna możliwa kubatura wszystkich wieżowców Bajhattanu. W przykładzie, kubatura wszystkich wieżowców wynosi 14, ale jeśli ich układ byłby nieco inny (ale panoramy wciąż takie same), kubatura mogłaby wynieść aż 22.
Input Format
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite $n$ oraz $m$ ($1 \le n, m \le 1\,000\,000$). Kolejny wiersz zawiera $n$ liczb całkowitych $z_{i}$ ($1 \le i \le n$), określających wysokości kolejnych wieżowców w panoramie zachodniej, począwszy od wieżowca najbardziej wysuniętego na północ. Trzeci wiersz zawiera $m$ liczb całkowitych $p_{j}$ ($1 \le j \le m$), określających wysokości kolejnych wieżowców w panoramie południowej, począwszy od wieżowca najbardziej wysuniętego na zachód. Możesz założyć, że $0 \le z_{i}, p_{j} \le 1\,000\,000$.
Output Format
Twój program powinien wypisać na wyjście maksymalną możliwą kubaturę Bajhattanu. Jeśli Bajtłomiej pomylił się (na przykład biorąc jedną panoramę Bajhattanu i jedną San Bajcisko, które również odwiedza) i zdjęcia nie mogą przedstawiać tego samego miasta, wypisz jedno słowo NIE.
Examples
Input
3 4 3 2 2 2 2 1 3
Output
22
Input 2
3 3 0 0 0 2 2 2
Output 2
NIE