King Byteasar is the ruler of the whole solar system that contains $n$ planets. This number is so large that people have abandoned the silly custom of naming the planets and use numbers instead. The planets are thus conveniently numbered from $1$ to $n$. Byteasar's palace is on the planet no. $1$, while his military base on the planet no. $2$. A long time ago Byteasar had a teleportation portal established between these two planets, which allows travelling from either planet to another in two hundred and fifty minutes (slightly over four hours).

Nowadays the teleportation technology is more mature, and the recent teleportation devices shorten the travel time to just a single hour. Let us note here, that all the portals, both the Byteasar's old one and the new ones available on the market, are of course bidirectional, and that the teleportation travel time is irrespective of the distance travelled. Some planets of the system are already connected with these new teleportation portals. In fact, it is already possible to travel between the planets no. $1$ and $2$ without using the king's private portal, though this involves several other portals and is thus no faster than the king's portal. Byteasar finds this rather fortunate, as he believes that such possibility would be a security breach.

The technology itself is increasingly available, and as everyone realises its economic significance, each pair of planets that are not currently directly connected with a portal are petitioning for establishing such a connection. Being a wise ruler, Byteasar intends to give his consent to as many constructions as possible, though keeping himself secure, i.e., not allowing the travel between planets $1$ and $2$ faster than with his private portal. Help the king determine how many portals he can agree to.

Input

Two integers are given in the first line of the standard input, $n$ and $m$ ($2 ≤ n ≤ 40\,000$, $0 ≤ m ≤ 1\,000\,000$), separated by a single space, denoting the number of planets in Byteasar's realm and the number of new portals that already exist. These teleportation portals are described in the $m$ lines that follow. Each such line contains two integers $a_i$ and $b_i$ ($1 ≤ a_i < b_i ≤ n$), separated by a single space, denoting that there is a teleportation portal of the new kind connecting $a_i$ and $b_i$. No pair of numbers appears twice. You may assume that the existing network of new portals allows travel from planet no. $1$ to planet no. $2$, but in no less than 250 minutes.

Output

Your program should print out just a single integer, namely the maximum number of portals Byteasar can agree to without breaching his security.

Example

Input

10 10
1 3
3 5
5 7
7 9
2 9
1 4
4 6
6 8
8 10
2 10

Output

10

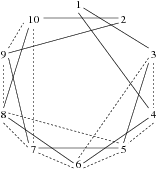
Existing portals are marked with solid lines, while those Byteasar can agree to with dashed lines.