Boss Rob planted $N$ happy little hazel trees in his yard (represented on a Cartesian plane). The $i$th tree is at integer coordinates $(X_i, Y_i)$. It's harvesting season, and Rob would like to set up some nets around the trees to collect the hazelnuts that fall. Each net must be an axis-aligned rectangle with integer vertices (on lattice points). Rob needs at least $1$ unit of space between nets so he can walk between them and collect the nuts. That is, nets cannot intersect, touch, or be nested. Each tree must lie strictly inside its net, i.e. must be at least $1$ unit away from the net's edge. Boss Rob can set up any number of nets, but would like to know the minimum total area of net required to cover all $N$ trees.
Constraints
- $1 \le T \le 160$
- $1 \le N \le 800,000$
- $0 \le X_i, Y_i \le 10^9$
- All $(X_i, Y_i)$ in a given test case are distinct.
$N > 500,000$ in at most two test cases.
The sum of $N$ over all test cases is at most $4,000,000$.
Input Format
Input begins with an integer $T$, the number of cases. For each case, there is first a line containing a single integer $N$. Then, $N$ lines follow, the $i$th of which contains two space-separated integers $X_i$ and $Y_i$.
Output Format
For the $i$th case, print a line containing "Case #i: " followed by a single integer, the minimum total area of net needed to enclose all trees according to the above requirements.
Sample Explanation
Solutions for the first two sample cases are depicted below.
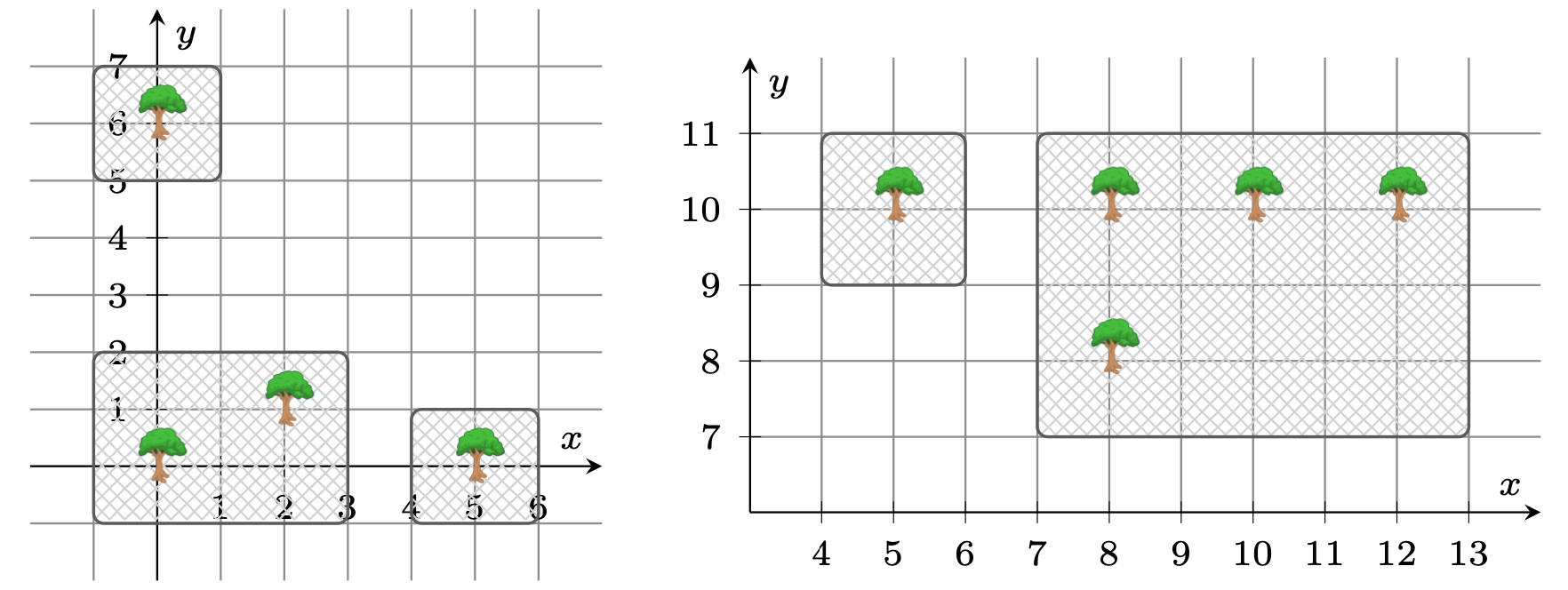
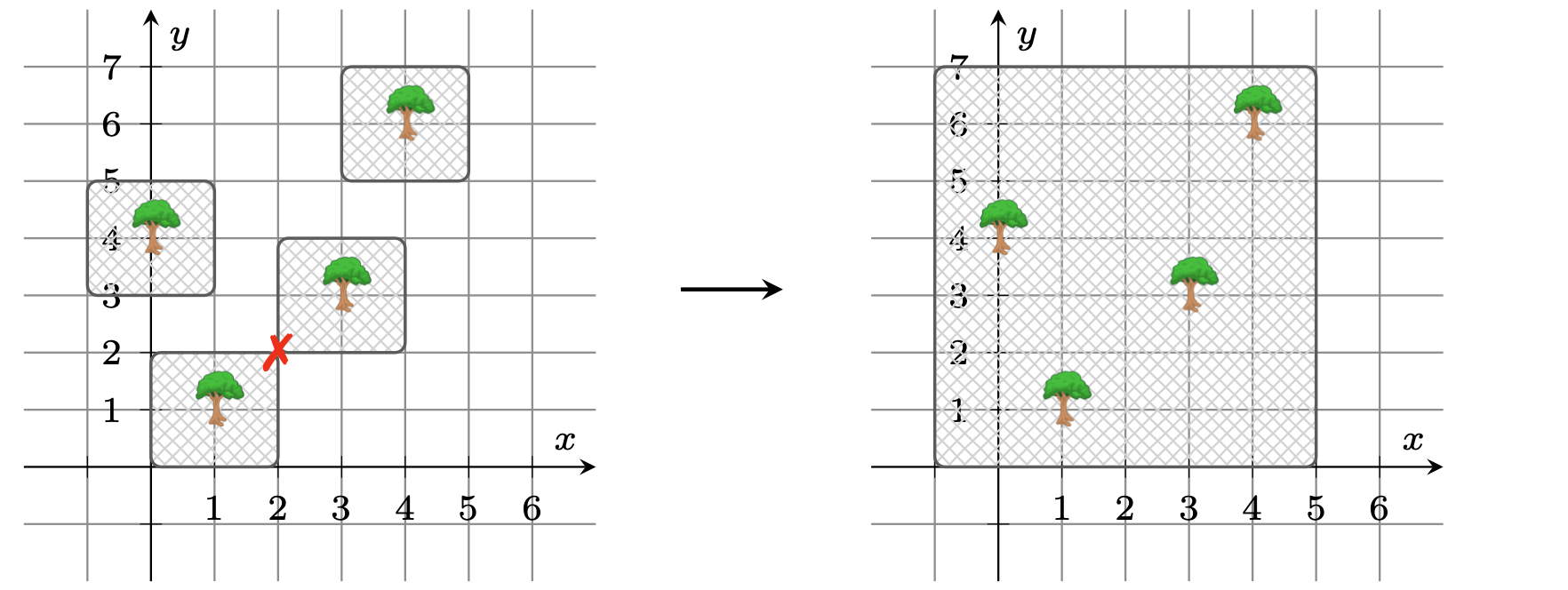
In the first case, the minimum possible net area is $2\times 2 + 3\times 4 + 2\times 2 = 20$. In the second case, the minimum possible net area is $2\times 2 + 4\times 6 = 28$. In the third case, it's almost possible to give each tree its own net. Unfortunately, there needs to be at least $1$ unit of space between the nets at $(2, 2)$ so Boss Rob can walk through. This makes it indirectly necessary to use one big net to cover all trees.
Sample Input
3 4 0 0 2 1 5 0 0 6 5 10 10 12 10 8 10 5 10 8 8 4 1 1 3 3 0 4 4 6
Sample Output
Case #1: 20 Case #2: 28 Case #3: 42