小 $y^\infty$ 看到了一道题:
给出一个长度为 $n$ 的序列 $A$,接下来有 $q$ 次操作,操作有四种:
1.对于所有的 $i\in[l,r]$,将 $A_i$ 变成 $A_i+x$。
2.对于所有的 $i\in[l,r]$,将 $A_i$ 变成 $x$。
3.对于所有的 $i\in[l,r]$,将 $A_i$ 变成 $\lfloor\sqrt{A_i}\rfloor$。
4.对于所有的 $i\in[l,r]$,询问 $A_i$ 的和。
保证$x > 0$。
作为一个数竞选手,小 $y^\infty$ 一眼就秒了这个题,这大约只要写一棵线段树就好了。
这里给出了他的详细做法,大概和 UOJ#228. 基础数据结构练习题 的做法差不多?
线段树是一种二叉树,它的每个节点都代表着一个区间,大约长这样:
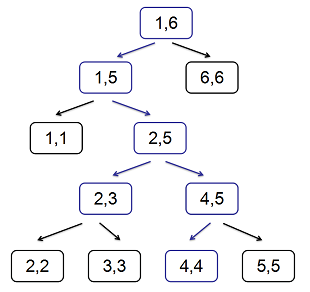
在每个节点上维护该区间的最小值,最大值和区间和。由于这个题(就是你在看的这个题)并不会询问这些值具体是多少,你可以认为它们和当前数列保持一致。反正是可以正确维护的就对了么
每个节点上会有一个标记二元组 $(a,b)$,若 $a=0$ 则为赋值标记,表示这个区间里的所有数都应被赋值为 $b$,若 $a=1$ 则为区间加标记,表示这个区间里的所有数都应被增加 $b$($x'=ax+b$)。最初,每个非节点上的标记都为 $(1,0)$,叶子节点的标记都为 $(0,A_i)$。
显然,这里的标记是可加的,标记 $(a_1,b_1)$ 加上标记 $(a_2,b_2)$ 的结果为:
$$\begin{equation}\left\{\begin{array}{lr}(0,b_2)&a_2=0;\\(a_1,b_1+b_2)&a_2=1.\\\end{array}\right.\end{equation}$$
当下传一个节点的标记时,先将该节点的标记分别加到左右孩子的标记上,然后再将该节点的标记赋值为 $(1,0)$。
要在节点 $[L,R]$ 将区间 $[l,r]$ 增加 $k$。若 $l\leq L \leq R\leq r$,那么给这个节点加上一个标记 $(1,k)$。否则,先下传该节点的标记,再递归与区间 $[l,r]$ 有交的孩子。每当有一个操作 $1$ 时,在节点 $[1,n]$ 将区间 $[l,r]$ 增加 $k$。
区间赋值是类似的,只不过加上的标记是 $(0,k)$。每当有一个操作 $2$ 时,在节点 $[1,n]$ 将区间 $[l,r]$ 修改为 $k$。
要在节点 $[L,R]$ 对区间 $[l,r]$ 开根号。若 $l\leq L\leq R\leq r$ 且 $max-min\leq 1$,当 $\lfloor\sqrt{max}\rfloor - \lfloor\sqrt{min}\rfloor = 0$ 时给这个节点加上一个标记 $(0,\lfloor\sqrt{min}\rfloor)$ ,当它等于 $1$ 时给这个节点加上一个标记 $(1,\lfloor\sqrt{min}\rfloor-min)$。否则,先下传该节点的标记,再递归与区间 $[l,r]$ 有交的孩子。每当有一个操作 $3$ 时,在节点 $[1,n]$ 给区间 $[l,r]$ 开根号。
显然,这样做的时间复杂度是均摊 $O(h\log\log A)$ 的,其中 $h$ 是线段树的树高,$A$ 是权值范围。
小 $y^\infty$ 很想知道每个节点的标记是什么。不过,作为一个数竞选手,他并不擅长写竞赛代码。他决定向你寻求帮助:你能回答他的问题吗?
请写一个程序,要求维护一棵用于维护数列 $A$ 的线段树,支持以下 4 种操作:
1.在节点 $[1,n]$ 将区间 $[l,r]$ 增加 $k$。
2.在节点 $[1,n]$ 将区间 $[l,r]$ 修改为 $k$。
3.在节点 $[1,n]$ 对区间 $[l,r]$ 开根号。
4.询问节点 $[l,r]$ 上的标记。
输入格式
第一行一个整数 $T$,表示测试点编号。
第二行两个整数 $n,q$,分别表示数列 $A$ 的长度与操作个数。
接下来一行 $n$ 个整数,表示数列 $A$ 的初值。
接下来一行包含 $n-1$ 个整数,按照先序遍历给出了该线段树所有非叶子节点的划分位置 $mid$ 。即,节点 $[l,r]$ 的左右孩子分别为 $[l,mid]$ 与 $[mid+1,r]$。不难发现通过这些信息就能唯一确定一棵 $[1,n]$ 上的线段树。
接下来的 $q$ 行,每行描述了一个操作,第一个数 $opt$ 表示操作类型。
若 $opt=1$,则表示执行了一个操作 $1$,接下来三个整数 $l,r,k$。
若 $opt=2$,则表示执行了一个操作 $2$,接下来三个整数 $l,r,k$。
若 $opt=3$,则表示执行了一个操作 $3$,接下来两个整数 $l,r$。
若 $opt=4$,则表示执行了一个操作 $4$,接下来两个整数 $l,r$。
输出格式
对于每个操作 $4$,输出一行两个整数 $a,b$,表示节点 $[l,r]$ 上的标记是 $(a,b)$。
样例一
input
0 6 7 1 1 1 1 1 1 5 1 3 2 4 2 2 5 2 4 2 5 1 2 4 1 4 2 5 4 2 3 4 4 4 4 5 5
output
0 2 1 0 0 3 0 3 0 2
限制与约定
共 $20$ 个测试点,每个测试点总分为 $5$ 分。
| 测试点编号 | 操作 $1$ | 操作 $2$ | 操作 $3$ | 操作 $4$ | 特性 $1$ | 特性 $2$ | |
|---|---|---|---|---|---|---|---|
| 1 | √ | √ | √ | √ | 划分线段树时有 $mid=\lfloor\frac{l+r}{2}\rfloor$ | ||
| 2 | √ | √ | √ | √ | 原线段树树高不超过 $30$ | ||
| 3 | √ | √ | √ | ||||
| 4 | √ | √ | √ | √ | |||
| 5 | √ | √ | √ | √ | |||
| 6 | √ | √ | √ | √ | √ | ||
| 7 | √ | √ | √ | √ | √ | √ | |
| 8 | √ | √ | √ | ||||
| 9 | √ | √ | √ | ||||
| 10 | √ | √ | √ | √ | |||
| 11 | √ | √ | √ | ||||
| 12 | √ | √ | √ | √ | √ | ||
| 13 | √ | √ | √ | ||||
| 14 | √ | √ | √ | ||||
| 15 | √ | √ | √ | √ | |||
| 16 | √ | √ | √ | √ | √ | ||
| 17 | √ | √ | |||||
| 18 | √ | √ | |||||
| 19 | √ | √ | √ | ||||
| 20 | √ | √ |
看!每个点都有特殊性质。
特性 $1$:划分线段树时有 $mid=l$ 或 $mid=r-1$。
特性 $2$:操作只会定位到一个节点,即,对于每个操作,其操作范围恰好是线段树的某个节点。
对于所有测试点,有:
$n = q = 10^5$,$A_i \leq 10^8$
操作 $1$ 保证 $k\leq 10^3$。
操作 $2$ 保证 $k\leq 10^8$。
部分分
显然,某个测试点错在第 $23333$ 行是一件游戏体验极差的事。作为一个有良心的出题人,本题将按照该点的正确率来给分:如果你的程序在某个测试点的正确率是 $p$,那么你将在此测试点得到$\frac{5(15^p-1)}{14}$ 分。另外,如果你输出的行数与标准答案行数不同,可能会爆零?没有testlib真自闭
没有输出时正确率当然为 1 啦!
什么,你说这是IOI赛制?我不听我不听,我要做良心出题人!
乱搞碾标算,N方过百万!