Interval tree can be regarded as an extension of traditional segment tree: each vertex in interval tree still represents a interval, but the split points do not need to be the middle point.
For example, the following picture describe an interval tree on $[1,6]$:
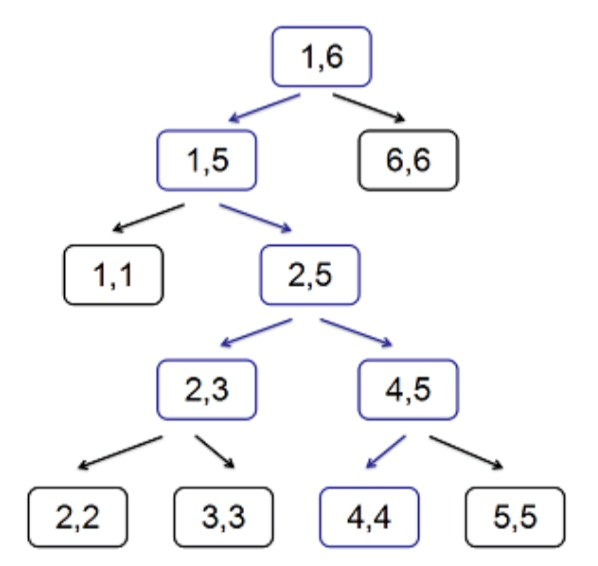
Similar with segment tree, we can do some interval queries on interval tree. And we can define the time complexity of interval $[l,r]$ as the number of vertices we need to visit when the query is about $[l,r]$.
Formally, let $S[l,r]$ be the set of vertices $v$ on the interval tree which satisfy one of the following 2 conditions:
- $v$'s interval is a subinterval of $[l,r]$, but $v$'s father's interval is not.
- At least one of $v$'s decendants satisfies (1).
And then, we can define the time complexity of $[l,r]$ as the size of $S[l,r]$.
For example, in the picture, all the vertices in $S[2,4]$ has been marked as blue. So the time complexity of $[2,4]$ in this interval tree is $6$.
Now, given an interval tree on $[1,n]$ and have $q$ queries. Each query is a positive integer $k$, you need to find out the number of different intervals of which the time complexity is exactly $k$.
Input
The input will consist of multiple test cases. Each case begins with two positive integer $n$ and $q$.
The second line contains $n-1$ integers, the split point of each non-leaf vertex, in the pre-order traversal. If vertex $[l,r]$'s split point is $m$, it's left child should be $[l,m]$ and it's right child should be $[m+1,r]$.
Then $q$ lines follow. The $i$-th line of the following $n$ lines is the integer $k$ denoting the $i$-th query.
The input guarantees that $l \leq m < r$, $1 \leq n,q \leq 10^5$, and $1 \leq k \leq 10^9$ and the sum of $n$'s and $q$'s in all test cases will not exceed $500\,000$.
Output
For each query, output a single line with a single number, the answer.
Example
Input
6 7 5 1 3 2 4 1 2 3 4 5 6 7
Output
1 2 2 3 6 4 3