九条可怜是一个贪玩的女孩子。
这天她在玩一个塔防小游戏。这个游戏的地图可以被看成一个二维平面,可怜已经建造了 $n$ 座防御塔,第 $i$ 座防御塔位于点 $A_i$,其坐标是 $(x_i,y_i)$。
防御塔需要有足够的能量才能运作,因此可怜需要选择一个位置 $O$ 建造能量源。当能量源建成后,第 $i$ 座防御塔的防御范围为以 $A_i$ 为圆心,过点 $O$ 的圆(包括边界)。
可怜发现,在建造了能量源之后,有些防御塔可能会变成冗余的。为了节约能源,她希望能在满足防御范围不变(即被至少一个防御塔的防御范围覆盖的区域不变)的情况下,拆除尽可能多的防御塔。
现在可怜有 $m$ 个能量源的建造方案 $O_i$,坐标为 $(a_i,b_i)$。 她希望你能对每一个建造方案,计算出最多能拆除多少座防御塔。
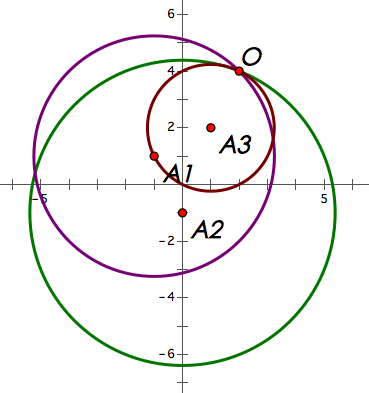
举例来说,当三个防御塔的坐标分为 $(-1,1),(0,-1),(1,2)$,能量源坐标为 $(2,4)$ 时,防御范围如下图所示。显然在最多只能拆除一座防御塔。
输入格式
第一行两个正整数 $n(n >1),m$。
接下来 $n$ 行每行两个整数 $x_i,y_i(|x_i|,|y_i| \leq 10^9)$,表示防御塔的坐标。
接下来 $m$ 行每行两个整数 $a_i,b_i(|a_i|,|b_i| \leq 10^9)$,表示一个建造方案。
数据保证所有点(包括防御塔坐标和建造方案)的横坐标两两不同,纵坐标两两不同。
输出格式
对于每个建造方案输出一行一个整数,表示在防御范围不变的情况下,最多能拆除多少座防御塔。
样例数据
样例 1 输入
4 2 0 -1 -1 1 1 2 2 4 -3 3 3 -2
样例 1 输出
2 1
子任务
本题分为 $4$ 个子任务,你需要通过所有子任务中的所有测试点,才能拿到这个子任务的分数:
子任务一($11$ 分),$n \leq 3, m \leq 100$。
子任务二($36$ 分),$n \leq 50, m \leq 100$。
子任务三($29$ 分),$n,m \leq 3000$。
子任务四($24$ 分),$n,m \leq 2 \times 10^5$.