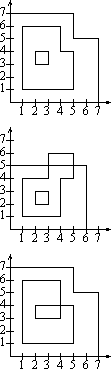
Let us consider a set of polygons with sides parallel to the axes of the coordinate system. Such a set of polygons is called a system of contour lines, if it is possible to order all the polygons of the set, so that the first polygon contains the second polygon in its interior, the second polygon contains the third polygon in its interior etc.
Your task is to check, if a given set of polygons is a system of contour lines.
Task
Write a program, which:
- reads descriptions of a few sets of polygons,
- for each set decides, if it is a system of contour lines,
- writes the result to the standard output.
Input
In the first line there is one natural number $t$ ($1 \le t \le 10$), denoting the number of sets to processed. Following, there are $t$ data sets. The first line of each data set contains one integer $n$ ($1 \le n \le 250$), denoting the number of polygons in this set. Each of the next $n$ lines contains one integer $m_i$ ($4 \le m_i \le 250$, $1 \le i \le n$), denoting the number of vertices of the $i$-th polygon, followed by $m_i$ pairs of integers $x_{i,j}$ and $y_{i,j}$ ($0 \le x_{i,j}, y_{i,j} \le 200\,000$), separated with a single space. These pairs describe coordinates of consecutive vertices of the polygon. The sides of each polygon are parallel to the axes of the coordinate system. Furthermore, no two adjacent sides of any polygon are collinear. The perimeter of any polygon does not contain self-crossings.
Output
The standard output should contain $t$ lines. The $k$-th line should contain one word TAK (i.e. yes in Polish), if the $k$-th set of polygons is a system of contour lines, NIE (i.e. no in Polish) otherwise.
Example
Input
3 3 6 1 1 5 1 5 4 4 4 4 6 1 6 6 0 0 0 7 5 7 5 5 7 5 7 0 4 2 3 3 3 3 4 2 4 3 4 2 2 3 2 3 3 2 3 8 1 1 1 4 3 4 3 6 5 6 5 4 4 4 4 1 4 0 0 6 0 6 5 0 5 3 6 1 1 5 1 5 4 4 4 4 6 1 6 6 0 0 0 7 5 7 5 5 7 5 7 0 4 2 3 4 3 4 4 2 4
Output
TAK NIE NIE