Lets consider a set $ S $ of $ n $ vertical segments on the plain (segments include their end points). None of the elements of $ S $ have a point in common. Two segments are said to "see each other" if there exists a horizontal segment, which connects them and does not have any common points with other segments from $ S $.
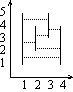
On the figure below, there is an example set of segments. Pairs of segments that can see each other, are: 1-2, 1-3, 2-3, 1-5 and 4-5. The segments 1 and 4 do not see each other.
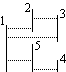
For a given number $ n $, we search for a set $ S $ of $ n $ vertical segments such that the number of pairs of segments which can see each other is as big as possible.
Write a program which:
- reads the number $ n $ from the standard input,
- computes locations of $ n $ vertical segments, such that
- none of them have a point in common,
- the number of pairs of segments which can see each other is as big as possible,
- writes the answer to the standard output.
Input Format
The first and only line of the standard input contains one integer $ n $ ($1 ≤ n ≤ 20\,000$).
Output Format
The first line of the standard output should contain one integer - maximal number of pairs of segments that can see each other. Each of the following $ n $ lines should identify the coordinates of one segment. Line $ i + 1 $ (for $ i = 1, 2, \ldots, n $) consists of three integers: $ x_{i} $, $ d_{i} $ and $ g_{i} $ ($0 ≤ x_{i} ≤ 1\,000\,000\,000$, $0 ≤ d_{i} < g_{i} ≤ 1\,000\,000\,000$), separated by a single space. They represent the segment which connects the points $( x_{i}, d_{i})$ and $(x_{i}, g_{i})$.
If there are more than one correct arrangement of $ n $ segments, your program can write out any of them.
Example
Input
4
Output
6 1 1 5 2 2 4 3 3 5 4 1 4