There are $n$ non-negative integers $a_1, a_2, \ldots, a_n$ arranged in a circle. The neighboring numbers in the circular order are $a_1$ and $a_2$, $a_2$ and $a_3$, $\ldots$, $a_{n-1}$ and $a_n$, $a_n$ and $a_1$.
Partition these numbers into three non-empty groups such that each number belongs to exactly one group, the numbers in each group are consecutively arranged in a circle, and the difference between the maximum and minimum sums of the numbers in the groups is minimized.
Input
The first line contains one integer $n$ $(3 \le n \le 10^6)$ -- the number of arranged numbers.
The second line contains $n$ non-negative integers $a_1, a_2, \ldots, a_n$ $(0 \le a_i \le 10^9)$ -- the numbers arranged in a circle.
Output
In the first line, output one integer -- the difference between the maximum and minimum sums of the numbers in the groups in the optimal partition.
In the second line, output three integers $x$, $y$, $z$ $(1 \le x < y < z \le n)$~--- such indices that the optimal partition of the numbers into three groups is of the form $[a_{x}, a_{x+1}, \ldots, a_{y-1}]$, $[a_{y}, a_{y+1}, \ldots, a_{z-1}]$, $[a_{z}, a_{z+1}, \ldots, a_{n-1}, a_{n}, a_{1}, a_{2}, \ldots, a_{x-1}]$.
If there are multiple correct answers, any of them is allowed to be output.
Example
Input
4 1 2 3 4
Output
1 1 3 4
Input
7 1 6 1 0 5 3 2
Output
0 2 3 6
Input
8 3 1 4 1 5 9 2 6
Output
1 3 6 8
Notes
In the third example, the optimal partition looks as follows:
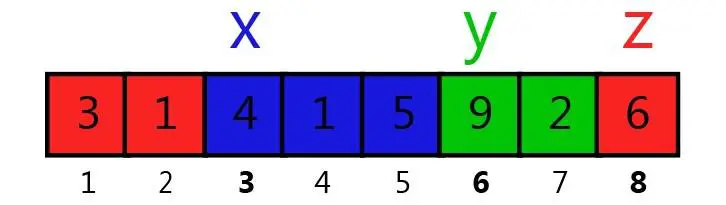
In this case, the sums in the groups are $10$, $11$, and $10$.
Scoring
- ($2$ points): $n = 3$;
- ($4$ points): $a_i \le 1$ for $1 \le i \le n$;
- ($13$ points): there exists a partition where the sought difference is equal to $0$;
- ($8$ points): $n \le 100$;
- ($9$ points): $n \le 2000$;
- ($13$ points): $n \le 5000$;
- ($28$ points): $n \le 10^5$;
- ($23$ points): with no additional restrictions.