This is an “output-only” problem. The test cases are made available to you. However, due to the large output size, you should still submit a program that reads the input and produces the outputs within the time limit.
Busy Beaver generated a random undirected graph with $N$ vertices and $M$ edges, where $M$ is a multiple of $3$. Now, he wants to partition the edges into $M/3$ paths of length $3$ (possibly starting and ending at the same vertex). Can you help Busy Beaver find such a partition?
Input
You can find the input files in the “Attachments” tab.
The first line of input contains two integers $N$ and $M$~--- the number of vertices and edges in the graph, respectively.
The $i$th of the next $M$ lines contains two integers $u_i$ and $v_i$ ($1 \le u_i,v_i \le N, u_i \ne v_i$)~--- the endpoints of the $i$th edge.
It is guaranteed that the $M$ edges were generated randomly. Formally, out of the $\frac{N(N-1)}{2}$ possible edges, $M$ distinct edges were chosen uniformly at random without replacement.
Output
Output $M/3$ lines. The $i$th line should contain $4$ integers $a_i$, $b_i$, $c_i$, and $d_i$ ($1 \le a_i,b_i,c_i,d_i \le N$), representing a path using edges $(a_i,b_i)$, $(b_i,c_i)$, and $(c_i,d_i)$.
It is allowed to have $a_i = d_i$. Your output should satisfy
$$ \bigcup_{i=1}^{M/3} \{\{a_i,b_i\},\{b_i,c_i\},\{c_i,d_i\}\} = \bigcup_{i=1}^M \{\{u_i,v_i\}\}. $$
Scoring
There are $10$ test cases in total, each worth $10$ points. For your convenience, the values of $N$ and $M$ in each test case are shown in the following list:
- Test $1$: $N = 771$, $M = 296835$.
- Test $2$: $N = 772$, $M = 297606$.
- Test $3$: $N = 1000$, $M = 300000$.
- Test $4$: $N = 3000$, $M = 300000$.
- Test $5$: $N = 10000$, $M = 300000$.
- Test $6$: $N = 30000$, $M = 300000$.
- Test $7$: $N = 50000$, $M = 300000$.
- Test $8$: $N = 70000$, $M = 300000$.
- Test $9$: $N = 80000$, $M = 300000$.
- Test $10$: $N = 90000$, $M = 300000$.
It is guaranteed that each of the $10$ generated graphs has a valid partition.
Example
Input
10 15 3 10 10 4 3 6 5 8 10 9 5 2 1 4 1 9 1 7 8 3 1 6 6 10 10 2 8 2 4 3
Output
2 5 8 2 8 3 10 2 3 4 1 7 6 1 9 10 3 6 10 4
Explanation
The sample is provided to illustrate the input and output format. It is not scored.
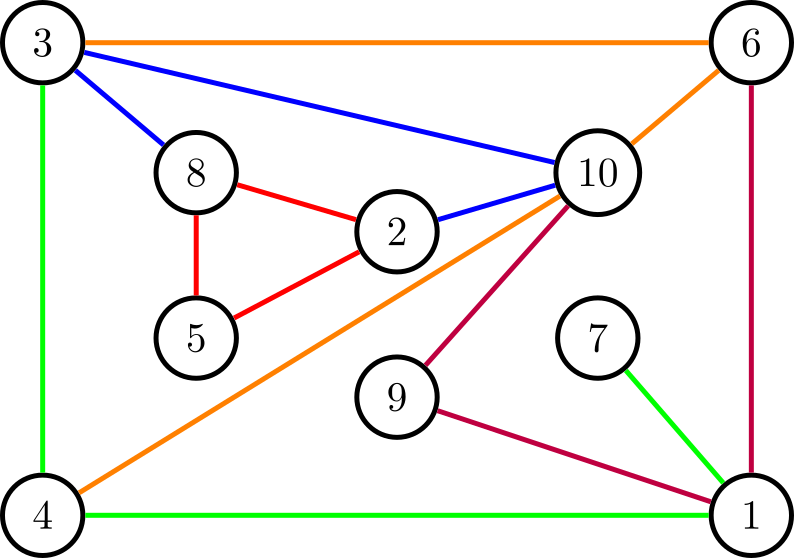
The sample graph and partition are shown in the figure below. Note that the path $2 - 5 - 8 - 2$ starts and ends at the same vertex, which is allowed.