Busy Beaver is visiting MIT, so he decided to have a tour around campus.
The campus consists of $N$ rooms and $N-1$ corridors between them. The rooms are enumerated consecutively from $1$ to $N$, and the $i$-th corridor has a known length $w_i$ and can be traversed in both directions. The layout of campus is also such that between any two rooms, there is exactly one way to go from one to another through these corridors without going through any room twice. Define the \textit{level} of a room to be the minimum number of corridors needed to get from the Great Dome (room $1$) to this room. For instance, the Great Dome is level $0$, and any room directly connected to it would be level $1$. Let $k$ be the highest level of any room on campus, and denote $d(u, v)$ to be the length of the shortest path between rooms $u, v$.
Busy Beaver wants his tour to be interesting. Starting from the Great Dome (room $1$), he wishes to visit a sequence of rooms $a_1, \dots, a_k$ such that for each $1 \leq i \leq k$, room $a_i$ is on level $i$, and for each $1 \leq i < k$, rooms $a_i, a_{i+1}$ are \textbf{not} connected by a corridor. As Busy Beaver is busy as usual, he also wants to minimize the total distance of the tour, which is $$d(1, a_1) + d(a_1, a_2) + \dots + d(a_{k-1}, a_k).$$
Since the MIT campus is very complex, Busy Beaver needs your help to plan out his tour. Help him find out the minimum length of an interesting tour.
Input
The first line consists of a single integer $N$ ($2 \le N \le 2 \cdot 10^5$) --- the number of rooms at the MIT campus.
Each of the next $N-1$ lines contains three integers $u$, $v$, $w$ ($1 \le u,v \le N$, $u \neq v$, $1 \le w \le 10^7$) --- a corridor between rooms $u$ and $v$ with the length $w$.
It is guaranteed that there is exactly one simple path between any two rooms, and that at least one interesting tour exists.
Output
Output a single integer, the minimal distance of an interesting MIT tour.
Scoring
There are three subtasks for this problem.
- ($15$ points): $N \le 10^3$.
- ($25$ points): $N \le 10^5$ and the maximum level of any room satisfies $k \leq 100$.
- ($60$ points): No additional constraints.
Examples
Input
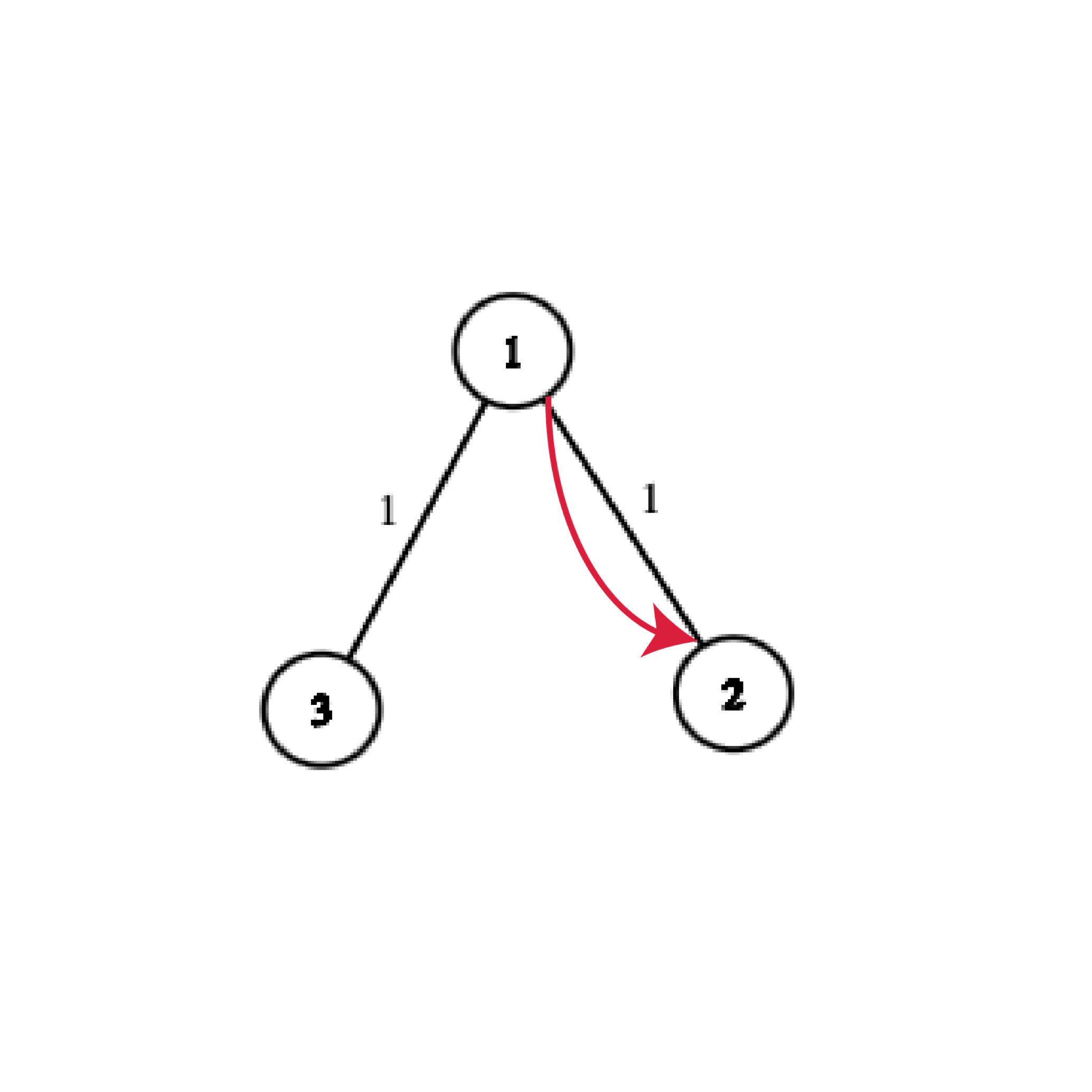
3 1 2 1 1 3 1
Output
1
Explanation
In the first test case, there are two possible interesting tours:
- $[a_1] = [2]$ --- The total distance of the tour will be $1$.
- $[a_1] = [3]$ --- The total distance of the tour will be $1$. They both obtain the minimum possible length of $1$, which is the answer for this case.
Input
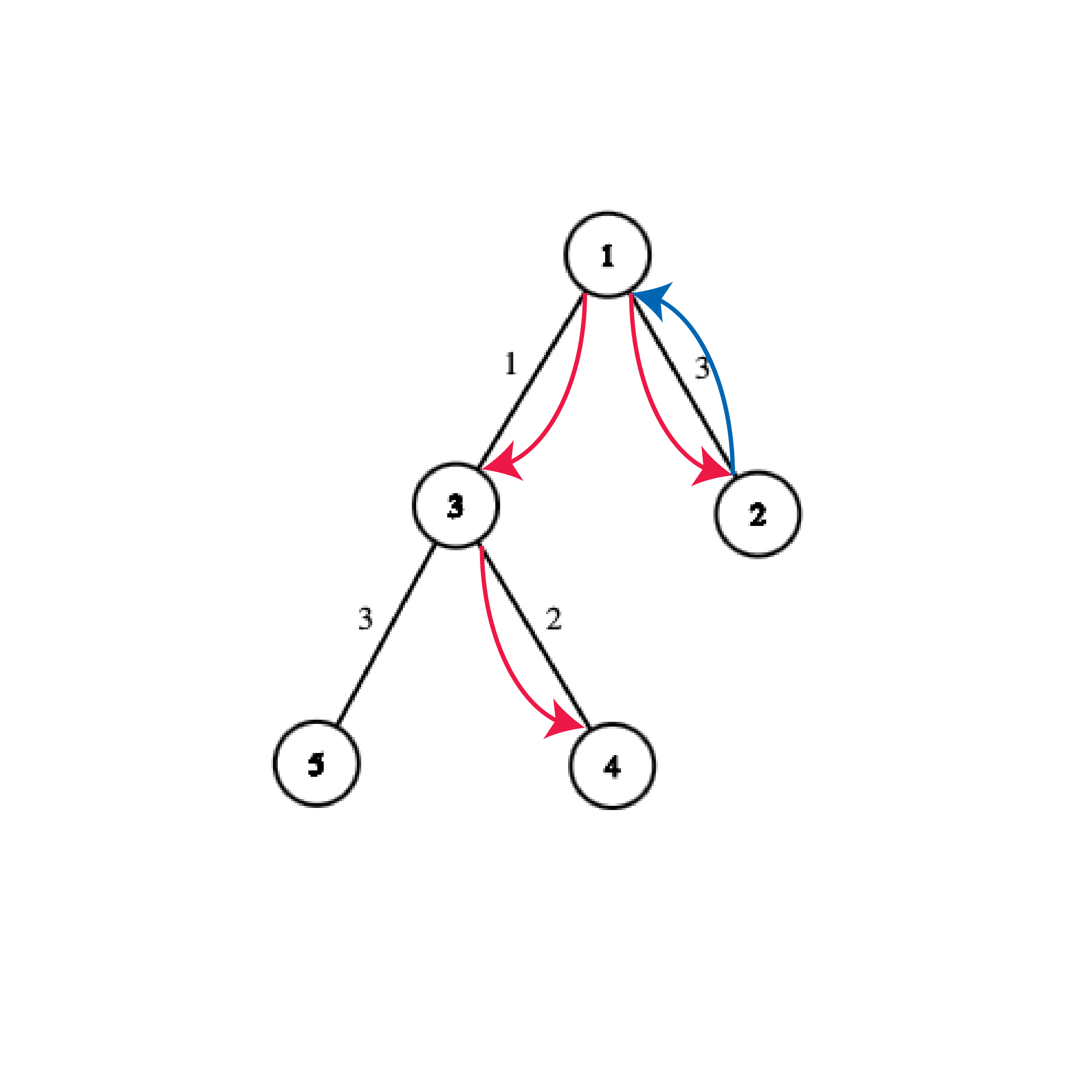
5 1 2 3 1 3 1 3 4 2 3 5 3
Output
9
Explanation
In the second test case, notice that both rooms of level $2$ are connected to room $3$. Therefore, no interesting tour can have $a_1 = 3$, or otherwise it will violate the condition that $a_1, a_2$ are not connected by a corridor. Therefore, there are two possible interesting tours:
- $[a_1, a_2] = [2, 4]$ --- The tour will traverse edges $1\rightarrow 2\rightarrow 1\rightarrow 3\rightarrow 4$. The total distance is $d(1, a_1) + d(a_1, a_2) = 3 + 6 = 9.$
- $[a_1, a_2] = [2, 5]$ --- The tour will traverse edges $1\rightarrow 2\rightarrow 1\rightarrow 3\rightarrow 5$. The total distance is $d(1, a_1) + d(a_1, a_2) = 3 + 7 = 10.$
Therefore, the minimum length of an interesting tour in this case is $9$.