题目描述
愚人节刚刚过去了,少女心不减的小松鼠却还想做一些更有意思的事情。
在小松鼠的教室里,有一堵纯白色的墙。这堵墙可以被看作$N$行$M$列的矩形网格。她计划依次进行$K$次刷墙操作。对于第$i$次操作,她都选择了连续的若干整行或者连续的若干整列,并把它们刷成颜色$c_i$(每种颜色可以表示为一个不同的非负整数,其中$0$表示白色)。
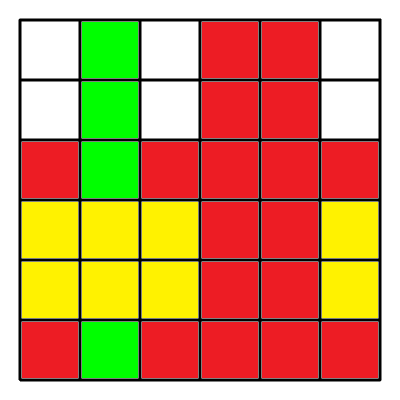
刷完之后的墙可能就是这个样子的!(对应着样例3)
在同一个格子上,后刷的颜色会完全覆盖掉之前的颜色。
请你帮助小松鼠满足她的好奇心,告诉她完成全部刷墙操作之后,有多少对相邻的格子颜色相同。
输入格式
第一行包含四个用空格隔开的非负整数 $N, M, K, q$($q \in \{0, 1\}$,见输出格式中的说明)。
对于接下来的$K$行,第$i$行包含四个用空格隔开的非负整数$type_i, l_i, r_i, c_i$ ($type_i \in \{0, 1\}$,$0 \leq c_i \leq K$),描述了一次刷墙操作。如果$type_i = 0$,表示她选择了第$l_i$行到第$r_i$行 ($1 \leq l_i \leq r_i \leq N$);如果$type_i = 1$,表示她选择了第$l_i$列到第$r_i$列 ($1 \leq l_i \leq r_i \leq M$)。
输出格式
一行一个整数。
如果$q = 0$,输出有多少对边相邻的格子颜色相同(边相邻即有公共边的格子);
如果$q = 1$,输出有多少对边相邻或角相邻的格子颜色相同(角相邻即有公共角的格子)。
样例输入与输出
样例1输入
3 4 3 1 0 2 3 2 1 3 3 0 1 2 2 1
样例1输出
8
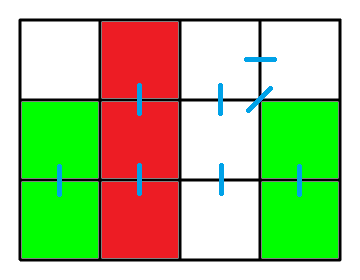
样例1说明
见下图。每条小短线对应着一对颜色相同的相邻格子。
样例2输入
5 4 1 1 1 2 4 0
样例2输出
55
样例3输入
6 6 4 0 0 3 6 1 1 2 2 2 0 4 5 4 1 4 5 1
样例3输出
33
数据范围与约定
对于全部测试点,$1 \leq N, M, K \leq 10^5$。
以下部分描述了每个测试点的详细信息。
| 测试点编号 | $N, M \leq$ | $K \leq$ | $q =$ | 其它约定 |
|---|---|---|---|---|
| 1 | $5000$ | $5000$ | $1$ | $l_i = r_i$ |
| 2 | $5000$ | $5000$ | $1$ | 无 |
| 3 | $5000$ | $10^5$ | $1$ | 无 |
| 4, 5 | $10^5$ | $10^5$ | $0$ | $l_i = r_i$ |
| 6, 7, 8 | $10^5$ | $10^5$ | $0$ | 无 |
| 9, 10 | $10^5$ | $5000$ | $1$ | 无 |
| 11, 12 | $10^5$ | $10^5$ | $1$ | $c_i = i$ |
| 13, 14, 15, 16 | $10^5$ | $10^5$ | $1$ | $c_i \in \{0, 1\}$ |
| 17, 18, 19, 20 | $10^5$ | $10^5$ | $1$ | 无 |