这是一道交互题。
题目背景
洞穴深处,布满青苔的老墙先是剧烈震动,扬起漫天尘土,随后大门徐徐向两侧移动。
门内的空气摆脱了百年的桎梏,争先恐后地直奔上来与昔日好友相会,把猝不及防的阿尔塔尔挤飞了两米远。
替代被吹灭的火炬为阿尔塔尔提供亮光的,是围绕着祭坛的宝石透出的璀璨光彩。
题目描述
祭坛呈正 $n$ 边形,每个顶点上有一个宝石。$n$ 种宝石与 $n$ 种能量一一对应,能量用 $1$ 至 $n$ 的整数编号。能量不一定按照对应的宝石在 $n$ 边形上的顺序编号。
$n$ 种能量中包含有 $(2n-3)$ 条双向的能量链接。这些能量链接对应到宝石上恰好构成了正 $n$ 边形和它的一个三角剖分。也就是说,
- 任何一条能量链接都连接不同的能量,且不会有两条能量链接连接相同的能量对;
- 祭坛上相邻的两个宝石对应的能量之间一定有能量链接;
- 同时,如果在包含能量链接的两种能量对应的宝石之间连上线段,那么任意两条线段都不在非顶点处相交,且把祭坛分成了 $(n-2)$ 个三角形。
阿尔塔尔只知道 $n$ 的值,既不知道每个宝石对应哪种能量,也不知道哪些能量之间形成了能量链接。
初始所有能量链接的状态都是未被摧毁,阿尔塔尔需要将这 $(2n-3)$ 对链接的状态均变为被摧毁。为此,阿尔塔尔可以进行以下几种操作,每种操作需要选择两种能量 $1 \le i,j \le n$:
- 能量感知:得到 $i$ 和 $j$ 最少需要多少对未被摧毁的能量链接才能联通;即,将宝石看作点、未被摧毁的能量链接看作边权为 $1$ 的无向边,那么会得到 $i$ 和 $j$ 的最短路长度。$i$ 和 $j$ 不连通时得到 $(n+1)$。
- 链接摧毁:需要保证 $i$ 和 $j$ 之间有一对能量链接且状态为未被摧毁,然后将其状态变为被摧毁。
- 链接重建:需要保证 $i$ 和 $j$ 之间有一对能量链接且状态为被摧毁,然后将其状态变为未被摧毁。由于会消耗大量体力,阿尔塔尔不能使用超过 $(2n-3)$ 次链接重建操作。
你需要帮助阿尔塔尔完成这个任务。使用能量感知的次数决定了阿尔塔尔的摧毁效率(也就是你的分数)。
实现细节
请确保你的程序开头有 #include "altar.h"
你不需要也不应该实现主函数。你需要实现以下函数:
void altar(int n);
- 其中 $n$ 表示祭坛的边数。
你可以调用以下函数:
int sense(int i, int j); bool destroy(int i, int j); void reconstruct(int i, int j);
- 这三个函数分别表示能量感知、链接摧毁、链接重建操作。你需要保证 $1 \le i, j \le n$。
- 对于
sense函数,其返回值为 $i$ 和 $j$ 的最短路长度;如果不连通返回 $(n+1)$。你需要保证调用sense的次数不超过 $5 \times 10^5$。 - 对于
destroy函数,如果在这一次链接摧毁操作后所有能量链接的状态都为被摧毁,返回true,否则返回false。 - 对于
reconstruct函数,你需要保证总调用次数不超过 $(2n-3)$。
- 对于
在满足题目条件和数据范围的情况下,交互库的运行时间不会超过 1500 ms,运行空间不会超过 64 MiB。
交互库不是自适应的,即能量链接和每个宝石对应的能量编号是固定的,不会随着交互过程改变。
测试程序方式
试题目录下的 grader.cpp 是我们提供的交互库参考实现,你可以忽略最终测试时所用的交互库实现与该参考实现的区别,但你不应该攻击交互库。
你需要在本题目录下使用如下命令编译得到可执行程序:
g++ grader.cpp sample.cpp -o sample -O2 --std=c++14 -lm
对于编译得到的可执行程序:
- 可执行文件将从标准输入读入以下格式的数据:
- 第一行一个整数 $n$ 表示祭坛边数。
- 接下来一行 $n$ 个整数 $p_1,p_2,\cdots ,p_n$,表示按照顺时针顺序,祭坛上每个宝石对应的能量编号。你需要保证这是一个 $1$ 到 $n$ 的排列。
- 接下来 $(n-3)$ 行每行两个整数 $i,j$,表示一对能量链接。你不需要输入形如 $(p_k, p_{(k \bmod n) + 1})$ 的能量链接。
- 读入完成之后,交互库将调用恰好一次函数
altar。 - 在
altar函数退出后,如果你在该函数中的所有调用满足题目条件,且所有能量链接都被摧毁,交互库将输出Correct. X,其中 $X$ 表示sense的调用次数;否则输出对应错误信息。
样例
输入
4
1 3 2 4
3 4输出
Correct. 0解释
该样例输出为下发的样例程序在该组样例下的输出。
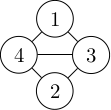
该样例中每个宝石对应的能量编号和能量链接如下图所示。
子任务
对于所有测试数据,$3 \le n \le 10^{3}$。
- 子任务 1(10 分):存在一种能量与其他所有能量都有链接。
- 子任务 2(10 分):将 $n$ 边形上的链接删去后,剩余的链接构成一个长度为 $(n-3)$ 的链。
- 子任务 3(30 分):该子任务共有 5 个测试点,数据按照如下方式生成:
- $n = 10^{3}$,$p_1, \cdots, p_n$ 在所有可能的排列中均匀随机生成;
- 按照如下方式生成三角剖分:对一个凸多边形,如果点数不超过 3 则退出;否则随机两个不相邻的顶点,在它们之间连边,并对该边分割的两个凸多边形递归处理。
- 子任务 4(50 分):无额外限制。该子任务依赖子任务 $1, 2, 3$。
评分方式
对于每个测试点,如果你的程序出现运行时错误,或超出了时间或空间限制,或程序中出现了非法的函数调用,或在函数结束时没有摧毁所有能量链接,你将获得该测试点 $0\%$ 的分数。否则你会按照 sense 的调用次数 $X$,依据如下公式计算该测试点的得分占比:
- 若 $X \in (10^5, 5 \times 10^5]$,你可以获得 $\left(5 + 15 \times \frac{5 \times 10^5 - X}{4 \times 10^5}\right) \%$ 的分数;
- 若 $X \in (10500, 10^5]$,你可以获得 $\left(20 + 30 \times \frac{10^5-X}{89500}\right) \%$ 的分数;
- 若 $X \in (3500, 10500]$,你可以获得 $\left(50 + 75 \times \left(\frac{3500}{X} - \frac{1}{3}\right)\right) \%$ 的分数;
- 若 $X \le 3500$,你可以获得该测试点 $100\%$ 的分数;
每个子任务的分数为该子任务中所有测试点的得分占比的最小值与该子任务满分的乘积。
后记
在摧毁了最后一对能量链接后,震动的大地和跌落的石块激起了阿尔塔尔的逃跑本能。
阿尔塔尔在洞穴坍塌的前一刻逃了出去。环顾四周,酣睡着的密林没有被惊醒,似乎什么都没有发生。
阿尔塔尔只是微微一笑:只不过和往常一样,世界只是忘记了回应。