我们知道一棵有根树可以进行深度优先遍历（DFS）以及广度优先遍历（BFS）来生成这棵树的 DFS 序以及 BFS 序。两棵不同的树的 DFS 序有可能相同，并且它们的 BFS 序也有可能相同，例如下面两棵树的 DFS 序都是 1 2 4 5 3，BFS 序都是 1 2 3 4 5。

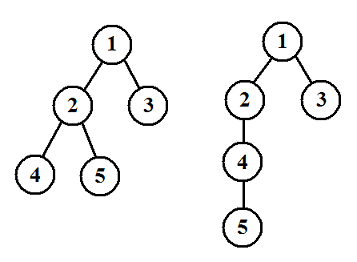
现给定一个 DFS 序和 BFS 序，我们想要知道，符合条件的有根树中，树的高度的平均值。即，假如共有 $K$ 棵不同的有根树具有这组 DFS 序和 BFS 序，且他们的高度分别是 $h_1,h_2, \dots ,h_K$，那么请你输出：

\begin{equation} \frac{h_1 + h_2 + \dots + h_K}{K} \end{equation}

输入格式

第一行包含 $1$ 个正整数 $n$，表示树的节点个数。

第二行包含 $n$ 个正整数，是一个 $1 \sim n$ 的排列，表示树的 DFS 序。

第三行包含 $n$ 个正整数，是一个 $1 \sim n$ 的排列，表示树的 BFS 序。

输入保证至少存在一棵树符合给定的两个序列。

输出格式

仅包含 $1$ 个实数，四舍五入保留恰好三位小数，表示树高的平均值。

样例一

input

5 
1 2 4 5 3 
1 2 3 4 5

output

3.500

限制与约定

如果输出文件的答案与标准输出的差不超过 $10^{-3}$，则将获得该测试点上的分数，否则不得分。

$20\%$ 的测试数据，满足：$n \leq 10$；

$40\%$ 的测试数据，满足：$n \leq 100$；

$85\%$ 的测试数据，满足：$n \leq 2000$；

$100\%$ 的测试数据，满足：$2 \leq n \leq 200000$。

说明

树的高度：一棵有根树如果只包含一个根节点，那么它的高度为 $1$。否则，它的高度为根节点的所有子树的高度的最大值加 $1$。

对于树中任意的三个节点 $a, b, c$，如果 $a, b$ 都是 $c$ 的儿子，则 $a, b$ 在 BFS 序中和 DFS 序中的相对前后位置是一致的，即要么 $a$ 都在 $b$ 的前方，要么 $a$ 都在 $b$ 的后方。