问题描述
在几何课上,老师画了一个圆,圆上有很多条弦,这些弦两两不重合,但是有些是相交的。你本想把图临摹下来回家好好研究,可惜下课后,图被值日生擦掉了。幸运的是,你准确地记录了弦的数量和弦的相交情况。
现在,你想尽量复原这张图。同时,你还想知道,最多能选出多少条弦,使得选出来的弦两两不相交。
输入格式
第一行包含 $2$ 个正整数 $n$,$m$,分别表示弦的条数以及相交弦的对数,所有的弦从 $1$ 至 $n$ 编号。
接下来 $m$ 行每行两个正整数 $a$,$b$,表示第 $a$ 条弦与第 $b$ 条弦相交。
输出格式
输出分为两行。
第一行输出 $2n$ 个正整数,按逆时针方向给出满足题意的圆上每条弦的两个端点的相对顺序,其中第 $i$ 条弦的两个端点均用数字 $i$ 来表示。
第二行输出 $1$ 个正整数,表示最多能选多少条两两不相交的弦。
样例输入
5 6
1 2
1 3
2 3
2 4
3 5
4 5样例输出
1 2 3 1 4 2 5 4 3 5
2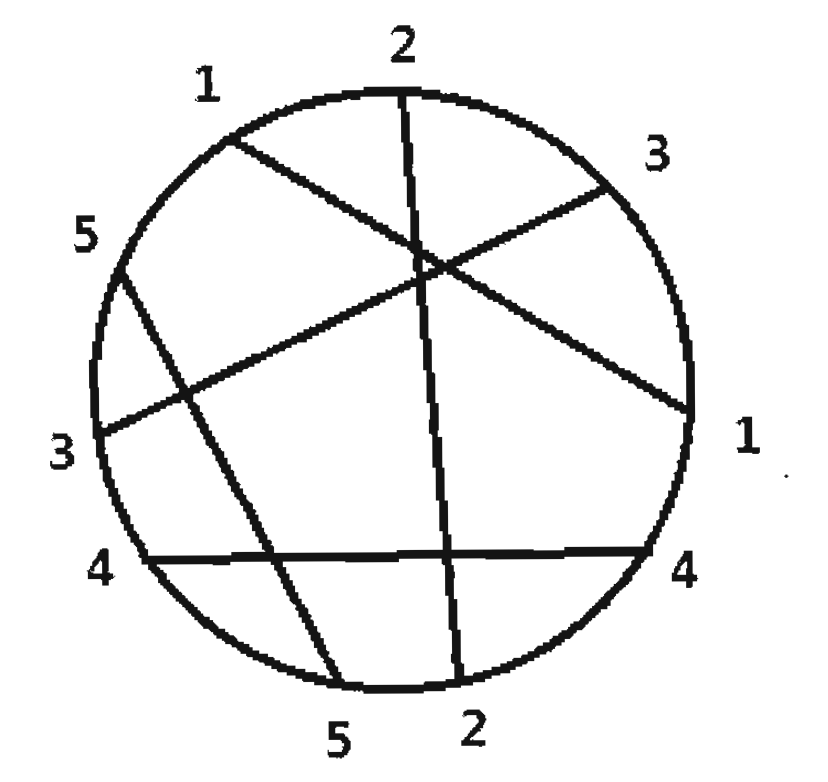
数据规模和约定
本题数据均为随机生成。没有在输入中出现的弦对均不相交。如果输出不合法,不得分。
对于 $10\%$ 的数据,$ 1 \leq n \leq 3 $;
对于 $30\%$ 的数据,$ 1 \leq n \leq 8 $;
对于 $40\%$ 的数据,$ 1 \leq n \leq 12 $;
对于 $60\%$ 的数据,$ 1 \leq n \leq 15 $;
对于 $75\%$ 的数据,$ 1 \leq n \leq 17 $;
对于 $95\%$ 的数据,$ 1 \leq n \leq 18 $;
对于 $100\%$ 的数据,$ 1 \leq n \leq 20 $,$ 1 \leq m \leq 40 $。