For his birthday present little Johnny has received from his parents a new plaything which consists of a tube and a set of disks. The aforementioned tube is of unusual shape. Namely, it is made of a certain number of cylinders (of equal height) with apertures of different diameters carved coaxially through them. The tube is closed at the bottom, open at the top. An exemplary tube consisting of cylinders whose apertures have the diameters: 5cm, 6cm, 4cm, 3cm, 6cm, 2cm and 3cm is presented in the image below.
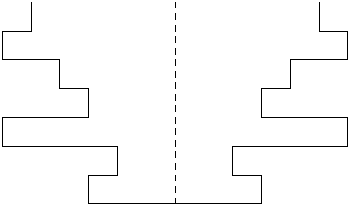
The disks in Johnny's plaything are cylinders of different diameters and height equal to those forming the tube.
Johnny has invented a following game: having a certain set of disks at his disposal, he seeks to find what depth the last of them would stop at, assuming that they are being thrown into the centre of the tube. If, for instance, we were to throw disks of consecutive diameters: 3cm, 2cm and 5cm, we would obtain the following situation:
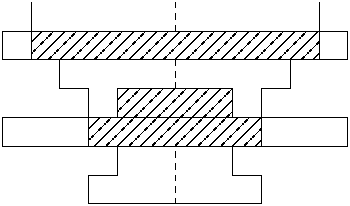
As you can see, upon being thrown in, every disk falls until it gets stuck (which means that it lies atop a cylinder, aperture of which has a diameter smaller than the diameter of the disk) or it is stopped by an obstacle: the bottom of the tube or another disk, which has already stopped.
The game being difficult, Johnny constantly asks his parents for help. As Johnny's parents do not like such intellectual games, they have asked you - an acquaintance of theirs and a programmer - to write a programme which will provide them with answers to Johnny's questions.
Task
Write a programme which:
- reads the description of the tube and the disks which Johnny will throw into it from the standard input,
- computes the depth which the last disk thrown by Johnny stops at,
- writes the outcome to the standard output.
Input
The first line of the standard input contains two integers $n$ and $m$ ($1 ≤ n,m ≤ 300\,000$) separated by a single space and denoting the height of Johnny's tube (the number of cylinders it comprises) and the number of disks Johnny intends to throw into it, respectively. The second line of the standard input contains $n$ integers $r_1,r_2,...,r_n$ ($1 ≤ r_i ≤ 1\,000\,000\,000$ for $1 ≤ i ≤ n$) separated by single spaces and denoting the diameters of the apertures carved through the consecutive cylinders (in top-down order), which the tube consists of. The third line contains $m$ integers $k_1,k_2,...,k_m$ ($1 ≤ k_j ≤ 1\,000\,000\,000$ for $1 ≤ j ≤ m$) separated by single spaces and denoting the diameters of consecutive disks which Johnny intends to throw into the tube.
Output
The first and only line of the standard output should contain a single integer denoting the depth which the last disk stops at. Should the disk not fall into the tube at all, the answer should be 0.
Example
Input
7 3 5 6 4 3 6 2 3 3 2 5
Output
2