九条可怜是一个热爱学习的女孩子。
今天她上了一门名叫集合论与图论的课程,在这门课中,她学到了一个名叫 "简单环" 的概念:
在有向图 $G=\langle V,E \rangle$ 中,简单环是一个点的序列 $a_1 \dots a_n(a_i \in V)$,满足:
- $a_1$ 是环中最小点,即$\forall 1 \leq i \leq n$,有 $a_1 \leq a_i$,这是为了避免将一个环统计多遍。
- $a_i$ 两两不同,即 $\forall 1 \leq i < j \leq n$,有 $a_i \neq a_j$.
- $a_i$ 连成了一个环,即 $\forall 1 \leq i < n$,有 $(a_i,a_{i+1}) \in E$,且 $(a_n,a_1) \in E$.
更进一步地,我们定义环 $a_1 \dots a_n$ 经过了边 $(u,v)$ 当且仅当$\exists i \in [1,n)$ 满足 $a_i=u,a_{i+1}=v$ 或者 $a_n=u,a_1=v$。
两个环是不同的当且仅当他们对应的点的序列不同。
在充分理解了简单环的概念之后,可怜出了一个简单的练习题:
给出一张有向图 $G$,设图 $G$ 中有 $p$ 个环 $c_i$,用如下方式构造无向图 $G'$:
- $G'$ 中有 $p$ 个点,和 $c_i$ 一一对应。注意在本题中对应关系可以任意的,他们并不影响答案。
- 点 $i$ 和点 $j$ 之间存在一条边当且仅当它们对应的环有至少一条公共边。
下图是一个例子,左图是一个 $4$ 个点的有向图,它有三个环 $(1,2,3),(2,3,4)$ 和 $(1,2,3,4)$,它对应的 $G'$ 如右图所示:
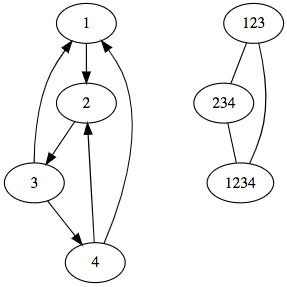
这个题对于可怜来说太难了,但是她相信这个题一定是能做的,于是她把这个题出到了这个比赛中,希望你能把她排忧解难 xD。
输入格式
第一行两个正整数 $n,m$ 表示 $G$ 的点数和边数。
接下来 $m$ 行,每行两个整数 $u_i,v_i(1 \leq u_i,v_i \leq n)$,表示图中的一条有向边。
输入保证图中不存在重边以及自环,注意一对点之间可能存在两条有向边,一条正向一条反向。
输出格式
输出一行一个整数,表示答案,即 $G'$ 中的联通块个数。
样例数据
样例 1 输入
4 6 1 2 2 3 3 4 4 1 3 1 4 2
样例 1 输出
1
样例 2 输入
6 9 1 2 2 3 3 4 4 2 3 1 4 5 3 6 5 6 6 5
样例 2 输出
2
子任务
本题分为 $3$ 个子任务,你需要通过所有子任务中的所有测试点,才能拿到这个子任务的分数:
子任务一($21$分):满足 $n \leq 10, m \leq 50$。
子任务二($46$分):满足 $n \leq 5000, m \leq 10^4$。
子任务三($33$分):满足 $n \leq 10^5, m \leq 2 \times 10^5$。