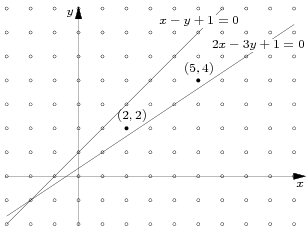
We are given six integers: $ A_{1}$, $ B_{1}$, $ C_{1}$, $ A_{2} $, $ B_{2} $, $ C_{2}$ such that $ A_{1}B_{2} ≠ A_{2}B_{1} $. These numbers are coefficients in equations of two intersecting lines:
- $ l_{1}: A_{1}x + B_{1}y + C_{1} = 0$,
- $ l_{2}: A_{2}x + B_{2}y + C_{2} = 0$.
The lines divide the plane into four parts. We represent each part by any point with integer coordinates, belonging to this part (but not belonging to any of the lines $ l_{1}$, $l_{2}$). You are given a point $(a, b)$ with integer coordinates representing one part. Find a point with integer coordinates $(c, d)$ representing the same part, such that its distance from the point of intersection of lines $ l_{1}$ and $l_{2}$ is least possible.
Write a program which:
- reads the equations of lines $l_{1}$ and $l_{2}$ and a point representing one part of plane,
- finds a point with integer coordinates representing the given part and closest to the point of intersection of lines $l_{1}$ and $l_{2}$,
- writes the answer to the standard output.
Input Format
The first line of the standard input contains three numbers $A_1$, $B_1$, $C_1$, separated by single spaces - the coefficients of $l_{1}$'s equation. The second line contains three numbers $A_2$, $B_2$, $C_2$, separated by single spaces - the coefficients of $l_{2}$'s equation. It is true that $ A_{1}B_{2} ≠ A_{2}B_{1}$. The third and last line contains two integers $ a $, $ b $, separated by a single space. They are the coordinates of a point representing one part of plane. Point $(a, b)$ does not belong to any of lines $l_{1}$, $ l_{2}$. For every number $ x $ from the input it is true that $-2\,100\,000\,000 < x < 2\,100\,000\,000$.
Output Format
Your program should write to the standard output two numbers $ c $, $ d $, separated by a single space - the coordinates of a point $(c,d)$ representing the given part, closest to the point of intersection of lines $l_1$ and $l_2$. If there are many such points, your program should output only one of them.
Example
Input
1 -1 1 2 -3 1 5 4
Output
2 2