There are $N$ cities numbered from $1$ to $N$, the $i$-th of which is at coordinates $(x_i, y_i)$.
Busy Beaver wants to start at city $1$, visit every city exactly once, and return to city $1$.
To go from city $i$ to city $j$, it takes $|x_i - x_j + y_i - y_j|$ seconds. Find the minimum number of seconds for Busy Beaver to complete his trip.
Input
The first line contains a single integer $T$ ($1 \leq T \leq 10^4$)~--- the number of test cases.
The first line of each test case contains a single integer $N$ ($2 \leq N \leq 2 \cdot 10^5$)~--- the number of cities.
The $i$-th of the next $N$ lines of each test case contains two integers $x_i$ and $y_i$ ($-10^9 \leq x_i, y_i \leq 10^9$)~--- the coordinates of the $i$-th city.
The sum of $N$ across all test cases does not exceed $2 \cdot 10^5$.
Output
For each test case, output a single integer~--- the minimum number of seconds needed for Busy Beaver to complete his trip.
Example
Input
3 5 0 0 -2 0 1 2 -1 3 0 1 3 0 0 1 4 3 4 2 -1 9 8 -4
Output
10 14 8
Explanation
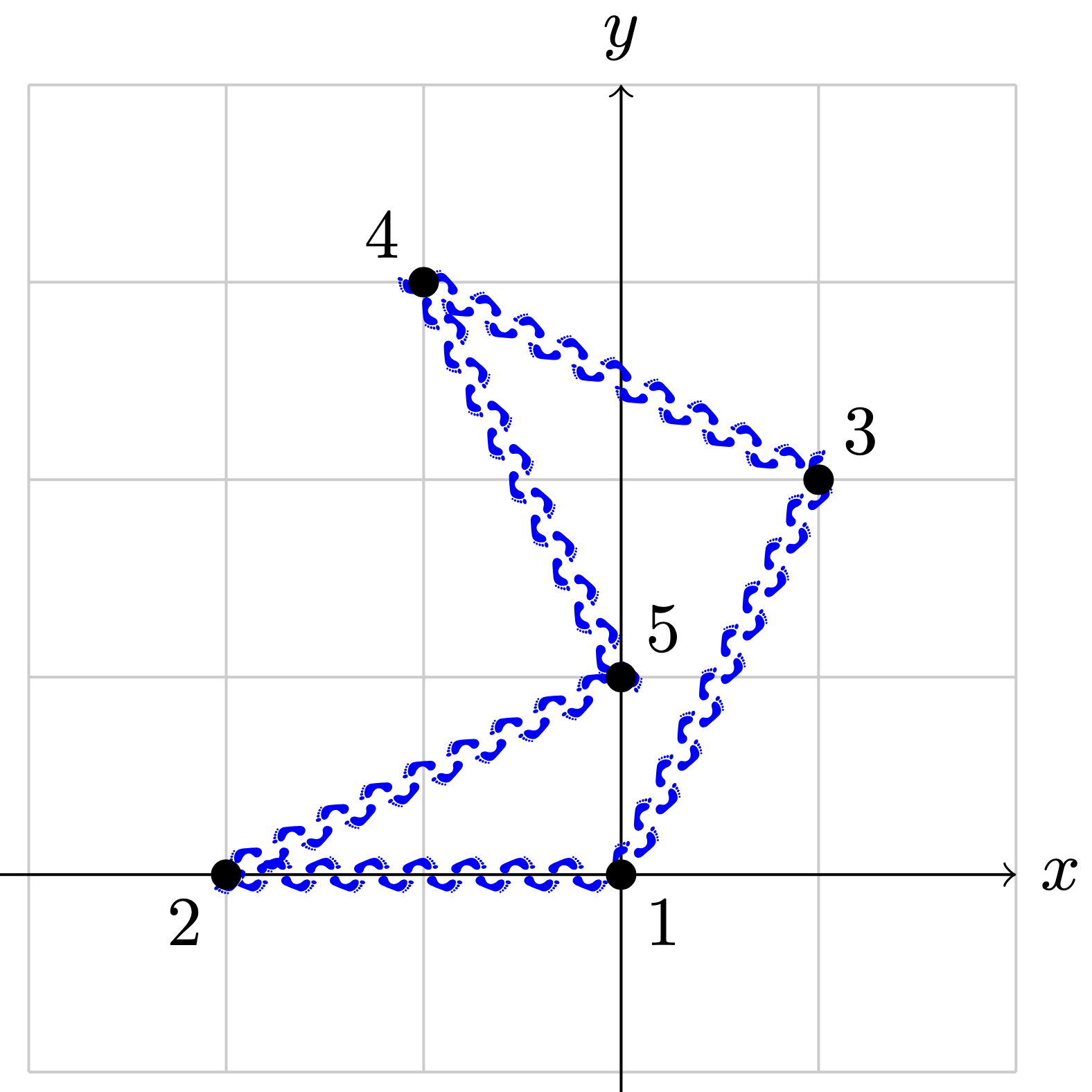
In the first test case, we can take the path $1 \xrightarrow{3\,\text{seconds}} 3 \xrightarrow{1\,\text{second}} 4 \xrightarrow{1\,\text{second}} 5 \xrightarrow{3\,\text{seconds}} 2 \xrightarrow{2\,\text{seconds}} 1$ which takes $3+1+1+3+2=10$ seconds.