Farmer John is training to become forklift certified! As part of his training, he needs to clear $N$ ($1 \le N \le 10^5$) boxes, conveniently labeled $1$ through $N$, from an old warehouse.
The boxes can be modeled as axis-aligned rectangles in a 2-dimensional plane, where the $+x$-direction is east and the $+y$-direction is north. Box $i$ has its southwest corner at $(x_{i1},y_{i1})$ and its northeast corner at $(x_{i2},y_{i2})$. All coordinates are integers in the range $[1, 2N]$, and no two corners from two different rectangles share the same $x$ or $y$ coordinate. All boxes have a non-zero area, and no two boxes intersect.
Farmer John plans to remove the boxes one at a time out of the southwest entrance of the warehouse. However, he can only remove a box if no part of any other box lies both south and west of the box's northeast corner due to physical limitations of the forklift.
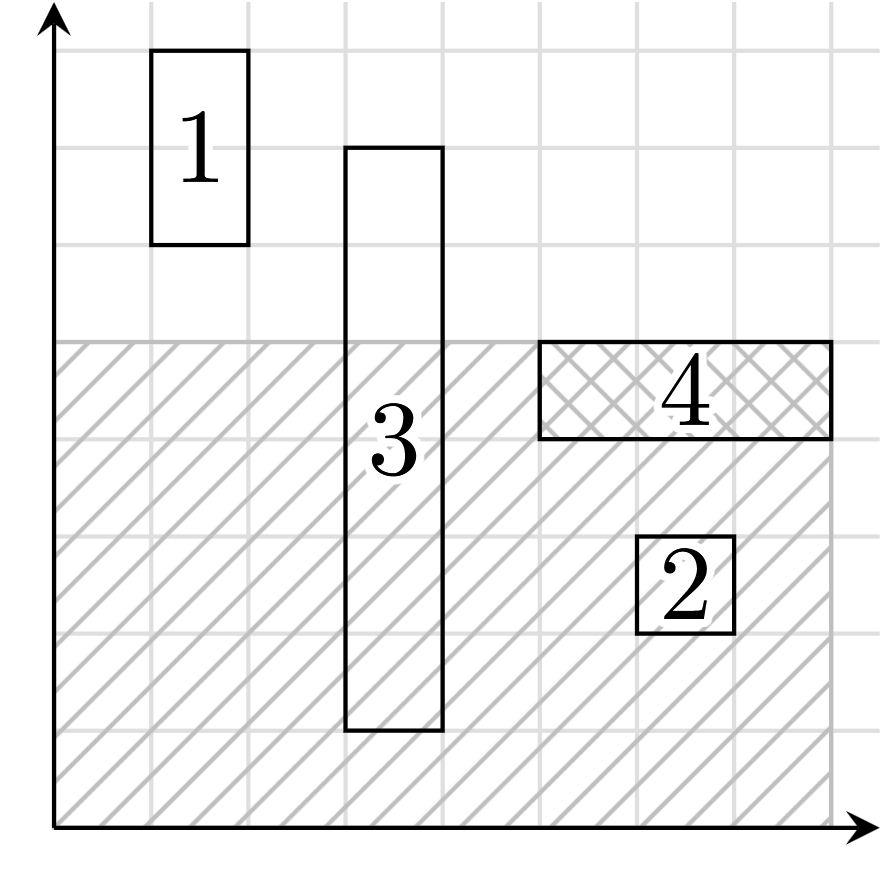
An example with $N=4$ is shown below. To remove box $4$, there cannot be any other boxes in the shaded region. Boxes $2$ and $3$ prevent box $4$ from being removed, but box $1$ does not.
Help Farmer John decide how to remove all the boxes! Your code should operate in two separate modes, defined by an integer flag $M$:
- Mode 1 ($M = 1$): Generate a permutation of $1, \dots, N$ specifying a valid box removal order. If there are multiple valid orders, find any. It can be proven that such an order always exists.
- Mode 2 ($M = 2$): For each $k = 1, \dots, N$, output $\texttt{1}$ if Farmer John can remove box $k$ if boxes $1, \dots, k - 1$ have already been removed, and $\texttt{0}$ otherwise.
Input Format
Each input consists of $T$ ($1 \le T \le 10$) independent test cases. It is guaranteed that the sum of all $N$ within each input does not exceed $5 \cdot 10^5$. The first line of input contains $T$ and $M$. (Note that $M$ is the same for each test case.) Each test case is then formatted as follows: The first line contains a single integer $N$.Each of the next $N$ lines contains four space-separated integers $x_{i1}, y_{i1}, x_{i2}, y_{i2}$: the locations of the southwest and northeast corners of box $i$.
- The first line of input contains $T$ and $M$. (Note that $M$ is the same for each test case.) Each test case is then formatted as follows: The first line contains a single integer $N$.
- Each of the next $N$ lines contains four space-separated integers $x_{i1}, y_{i1}, x_{i2}, y_{i2}$: the locations of the southwest and northeast corners of box $i$.
Output Format
For each test case:
- If $M = 1$, output a single line with $N$ space-separated integers, where the $j$-th integer is the label of the $j$-th box to remove.
- If $M = 2$, output a single line with a binary string of $N$ characters specifying the answer for each $k = 1, \dots, N$.
Sample Data
Sample Input
2 1 4 1 6 2 8 6 2 7 3 3 1 4 7 5 4 8 5 3 1 5 3 6 4 1 5 2 2 3 6 4
Sample Output
1 3 2 4 2 3 1
Sample Input 2
2 2 4 1 6 2 8 6 2 7 3 3 1 4 7 5 4 8 5 3 1 5 3 6 4 1 5 2 2 3 6 4
Sample Output 2
1011 011
Sample Explanation
For the first test case, box $2$ is blocked by box $3$, so Farmer John cannot remove it before removing box $3$.
Constraints
- Inputs 3-5: $M = 1$, $N\le 1000$.
- Input 6: $M = 2$, $N \le 1000$.
- Inputs 7-13: $M = 1$, no additional constraints.
- Inputs 14-16: $M = 2$, no additional constraints.